Simulated Games
In this document we describe the concept of Simulated Games used in Grail.
Simulated Games - the underlying technique
This is an algorithm that takes advantage of a game simulator. The simulator is responsible for checking various ways the game may unfold in order to find the most promising actions. Under the hood, we use an algorithm called Monte Carlo Tree Search (MCTS) slightly modified to make it more applicable in real-time video games. If you are interested in the theory behind it, we recommend an excellent survey paper.
However, theoretical background is not required in order to use this technique in Grail. We provide the necessary details, but it is advised to at least examine all of our examples and play around with various ways Simulated Games can be designed. This will not only make your bots stronger/more interesting, but you will also have more intuition in working with this algorithm in your next games.
The MCTS algorithm is a simulation-based technique that tests various playouts of a game and gathers statistics. The more time it gets for computations, the better (more accurate) statistics it will provide. It is an anytime algorithm meaning that it can be stopped at anytime and it will provide the currently best actions. In particular, it can be time-sliced - the computations do not have to be performed in one go. The SimulatedGameReasoner comes ready with time-slicing.
The algorithm consists of four phases:
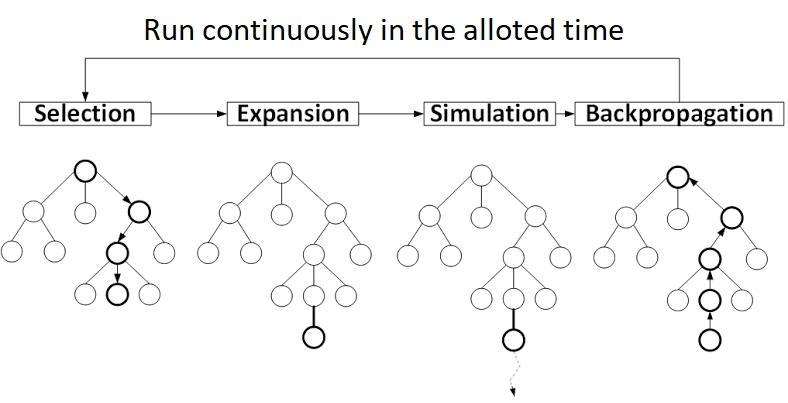
-
Selection - the algorithm always starts from the root node and traverses the cached in-memory representation of the game tree trying underexplored or new action sequences as well as double checking the most promising lines found so far. This is know as the exploration vs. exploitaion problem and MCTS does it really well. At some point, the algorithm will fall out of the tree and then the selection phase ends.
-
Expansion - a new node that resembles the first action performed after the selection phase is added to the tree.
-
Simulation - we are in some state that occured after adding a new node to the tree. Now the algorithm simulates the game randomly until the termination condition is met.
-
Backpropagation - the game results are calculated and propagated to all actions performed in the selection and expansion phases. The statistics are updated.
| It is common to use the term simulation for the whole iteration of MCTS. The selection phase can be viewed as an informed and guided part of such simulation, whereas the actual simulation phase is an exploratory unguided part. |
State representation
In the MCTS algorithm, the state of the game is often stored explicitly in tree nodes. In the Simulated Games module, we do not store the game state at all. Instead, only a temporary state (the so-called rolling state) is maintained for the simulation purposes.
However, there is no dedicated class that represents the game state.
The actual state is made of internal states of all units (SimulatedGameThinkingUnit and SimulatedGameStochasticUnit) defined in the game. The difference between the two types of units is documented in Simulated Games - defining a game in 10 steps and in the API reference (links on the bottom of the page). However, just to recap: SimulatedGameThinkingUnit is considered to maximize its reward, therefore, the algorithm will simulate it using the selection formula that chooses more promising actions more often. The SimulatedGameStochasticUnit does not have any reward and does not make actions according to its choice but rather a probability distribution.
Simulated Games - selection in Grail
Each iteration starts from the initial state (the actual state of the game).
| It is important to provide a proper implementation of the reset function, which reverts state of each unit to the starting one. Whenever actions change something, it should be reverted to in one of the reset functions. |
Another thing MCTS does here is asking units for their available actions and caching them.
| It is important to return list of actions and not modify them afterwards. |
If any sequence of actions chosen by MCTS is repeated, then the algorithm assumes that we are in the same state as before. It will use the cached available actions obtained previously when the same sequence of actions was performed.
| It is important that effects of actions are either deterministic or do not affect future legality of units' actions. If your actions have non-deterministic nature, use SimulatedGameStochasticUnit. Each possible outcome is an action of such a unit. |
| In general, the selection algorithm will check all the available actions. However, you can provide heuristics that know better which action should be chosen when certain conditions/criteria are met. Those heuristics are called HeuristicReasoners. |
The most significantly related functions:
-
C++
-
C#
grail::simgames::ISimulatedGameUnit::Reset()
grail::simgames::ISimulatedGameUnit::GetAvailableActions()
grail::simgames::ISimulatedGameUnit::HeuristicReasonersISimulatedGameUnit.Reset()
ISimulatedGameUnit.GetAvailableActions()
ISimulatedGameUnit.HeuristicReasonersSimulated Games - expansion in Grail
Nothing special here. Just make sure again that the returned available actions will not be modified anymore, so they will be cached in the newly expanded node.
Simulated Games - simulation in Grail
The simulation phase is similar to the selection one, but actions are not cached here and there is uniform random selection. In the selection phase, the algorithm looks at all actions and selects the most promising to test next. In the simulation phase - just one action is enough. It should be either (1) - fully random or (2) - the best one if there is clear best action or (3) - sometimes random and sometimes the best one.
In order to make simulation efficient you might provide an optimized override for the function. The default implementation will just compute all available actions and choose one randomly with equal probability for each of them.
-
C++
-
C#
grail::simgames::ISimulatedGameUnit::GetRandomAvailableAction(RandomGenerator& rand_gen)ISimulatedGameUnit.GetRandomAvailableAction(Random random)Simulated Games - backpropagation in Grail
The backpropagation is done when the game is terminated. You should request for termination by setting the appropriate flag.
| The request for termination is typically set either as part of an action or in the AfterAction function. |
In this phase, the algorithm will check the scores set to each player. The scores represent the game outcome.
| The scores are typically set in the same place where reqest for termination is set to true. |
The most significantly related functions:
-
C++
-
C#
grail::simgames::SimulatedGameRuntime::SetTerminationRequest() //call when the game reached the end
grail::simgames::SimulatedGameRuntime::SetScore(int player, float score) //set the game result for the team
grail::simgames::SimulatedGameRuntime::GetScore(int player) //getter for above
grail::simgames::SimulatedGameThinkingUnit::GetTeamIndex() //the team (player) of the unit
grail::simgames::SimulatedGameThinkingUnit::AfterAction() //called after any actionSimulatedGameRuntime.TerminationRequest //set when the game reached the end
SimulatedGameRuntime.Scores //set the game result for the team
SimulatedGameThinkingUnit.TeamIndex //the team (player) of the unit
SimulatedGameThinkingUnit.AfrerAction(...) //called after any action| The scores array corresponds to the indices of teams set for units. Units of the same team share the score. This allows for their coordination in working towards the same goal. |